Zhipei Yan (颜智培)

Control of Curvature Extrema in Curve Modeling

PhD Dissertation

[pdf] [slides]

We present a method for constructing almost-everywhere curvature-continuous curves that interpolate a list of control points and have local maxima of curvature only at the control points. Our premise is that salient features of the curve should occur only at control points to avoid the creation of features unintended by the artist. While many artists prefer to use interpolated control points, the creation of artifacts, such as loops and cusps, away from control points has limited the use of these types of curves. By enforcing the maximum curvature property, loops and cusps cannot be created unless the artist intends to create such features.

To create these curves, we analyze the curvature monotonicity of quadratic, rational quadratic and cubic curves and develop a framework to connect such curve primitives with curvature continuity. We formulate an energy to encode the desired properties in a boxed constrained optimization and provide a fast method of estimating the solution through a numerical optimization. The optimized curve can serve as a real-time curve modeling tool in art design applications.

NanoCommunication-based Flow Path Mapping for NanoSensors in Underground Oil Reservoirs

Jin L., Yan Z., Zuo L. and Stoleru R.

ACM International Conference on Nanoscale Computing and Communication (NanoCom), 2020

[pdf]

Oil reservoir exploration is booming, given the increasing energy demand worldwide. The existence of Impermeable Regions (IR) in the oil reservoir (i.e., underground areas that allow only few hydrocarbons-collecting fluid to pass through) still hinders current production performance to a great extent. Research efforts have been invested into IR detection and mapping. The state of the art solution leverages nanoscale sensor networks to approximately characterize the location of a single IR in the underground oil reservoir. However, the characterization accuracy is rather low. In addition, existing solutions are not applicable to more heterogeneous reservoirs, which reflects, in fact, a more realistic problem scenario. In this paper, we investigate and address the limitations of state of the art solutions in two aspects: 1) we provide a sub-terahertz (THz) communication channel to reflect realism of nanocommunication in the underground; 2) we develop a sensor path (i.e., simulated streamlines along which sensors are assumed to flow) reconstruction workflow to map a more heterogeneous reservoir with more IRs. Through simulations, we show that our proposed solution achieves an improvement of IRs mapping performance, when compared to the state of the art solution.

NanoCommunication-based Impermeable Region Mapping for Oil Reservoir Exploration

Jin L., Zuo L., Yan Z. and Stoleru R.

ACM International Conference on Nanoscale Computing and Communication (NanoCom), 2019

[pdf]

Oil continues to play a significant role in providing worldwide energy. Impermeable zones (i.e., underground areas that allow only few hydrocarbons-collecting fluids, to pass through) can cause significant challenges during the drilling and oil production periods. The problem of mapping an impermeable area has been investigated mainly using seismic sensors deployed on the Earth surface. The existing solutions continue to be imprecise. In this paper we propose a solution that employs nanodevices enabled with wireless THz communication capabilities. The nanodevices are deployed underground and collected as part of oil exploration and recovery. Wireless connectivity among nanodevices is used for mapping underground flow propagation paths, and implicitely, impermeable areas. Since the deployment underground of nanodevices is costly, in this paper we aim to reduce the number insertion and collection/production wells. Through simulations, we show that our proposed solution achieves good accuracy in mapping impermeable zones, with a reduced cost.

A Family of Barycentric Coordinates for Co-Dimension 1 Manifolds with Simplicial Facets

Yan Z. and Schaefer S.

Computer Graphics Forum (Proceedings of the Symposium on Geometry Processing), Vol. 38, No. 5 (2019), pp. 075-083

[pdf] [slides] [code (soon)]

We construct a family of barycentric coordinates for 2D shapes including non-convex shapes, shapes with boundaries, and skeletons. Furthermore, we extend these coordinates to 3D and arbitrary dimension. Our approach modifies the construction of the Floater-Hormann-Kós family of barycentric coordinates for 2D convex shapes. We show why such coordinates are restricted to convex shapes and show how to modify these coordinates to extend to discrete manifolds of co-dimension 1 whose boundaries are composed of simplicial facets. Our coordinates are well-defined everywhere (no poles) and easy to evaluate. While our construction is widely applicable to many domains, we show several examples related to image and mesh deformation.

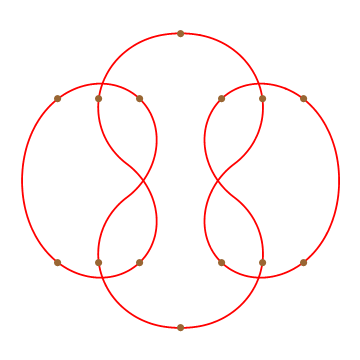
Circle Reproduction with Interpolatory Curves at LocalMaximal Curvature Points

Yan Z., Schiller S. and Schaefer S.

Computer Aided Geometric Design, Vol. 72, No. 6 (2019), pages 98-110

[pdf] [code]

We present a piece-wise rational, quadratic, interpolatory curve that is able to reproduce circles and other elliptical or hyperbolic shapes. The curve is curvature continuous except at infection points and points of local maximum curvature appear only at control points and nowhere else. The local maximum curvature property ensures that users have direct control over salient points of the curve, and users can control if and where features such as cusps and loops are generated.

To construct the desired curve, we formulated an energy that encodes the desired properties to optimize using a boxed constrained optimization. We provide an efficient algorithm for choosing an initial guess close to the solution to accelerate convergence. In addition, we show how to automatically choose the rational weights of the curve as part of the optimization to reproduce shapes such as circles.

κ-Curves: Interpolation at Local Maximum Curvature

Yan Z., Schiller S., Wilensky G., Carr N., and Schaefer S.

ACM Transactions on Graphics (Proceedings of SIGGRAPH), Vol. 36, No. 4, (2017), pp. 129:1-129:7

[pdf] [slides] [github, Mathematica(.nb), C++]

We present a method for constructing almost-everywhere curvature-continuous, piecewise-quadratic curves that interpolate a list of control points and have local maxima of curvature only at the control points. Our premise is that salient features of the curve should occur only at control points to avoid the creation of features unintended by the artist. While many artists prefer to use interpolated control points, the creation of artifacts, such as loops and cusps, away from control points has limited the use of these types of curves. By enforcing the maximum curvature property, loops and cusps cannot be created unless the artist intends for them to be.

To create such curves, we focus on piecewise quadratic curves, which can have only one maximum curvature point. We provide a simple, iterative optimization that creates quadratic curves, one per interior control point, that meet with G² continuity everywhere except at inflection points of the curve where the curves are G¹. Despite the nonlinear nature of curvature, our curves only obtain local maxima of the absolute value of curvature only at interpolated control points.

Shoot 'em Up Game in Mathematica, v2

This is a remake version of my previous "Simple Raiden" game implemented in Wolfram Mathematica. Run all sections and drag the orange spot to control the player. You have 3 lives. Rock 'n' roll, shoot the fighters and tanks!

3D Scanning

3D portrait scanning using Kinect XBox 360. Delete all inner and invisible triangles and fill some of the holes.

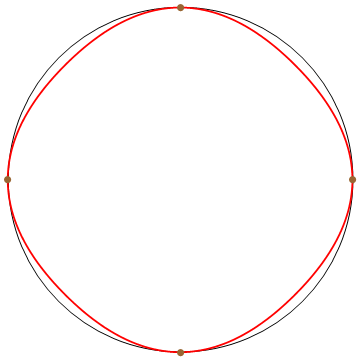
Improved κ-Curves

An attempt to reproduce circles on κ-Curves using functional maps.

Implementation of Mipmap

An implementation of mipmap for multi-level texture mapping.

Implementation of Marching Cubes

An implementation of Marching Cubes in Mathematica on the Stanford bunny point cloud data.

High Genius Sculpture Model

A high genius sculpture model, generated by TopMod and 3D printed.

[Model (.obj)] [More Pictures] [Course Page]

Distributed Ray Tracer

A ray tracer with reflection, refraction, environment map, normal map, motion blur, out of focus, translucent effect, and etc

Examples: static motion

[HiRes] [Course Page]

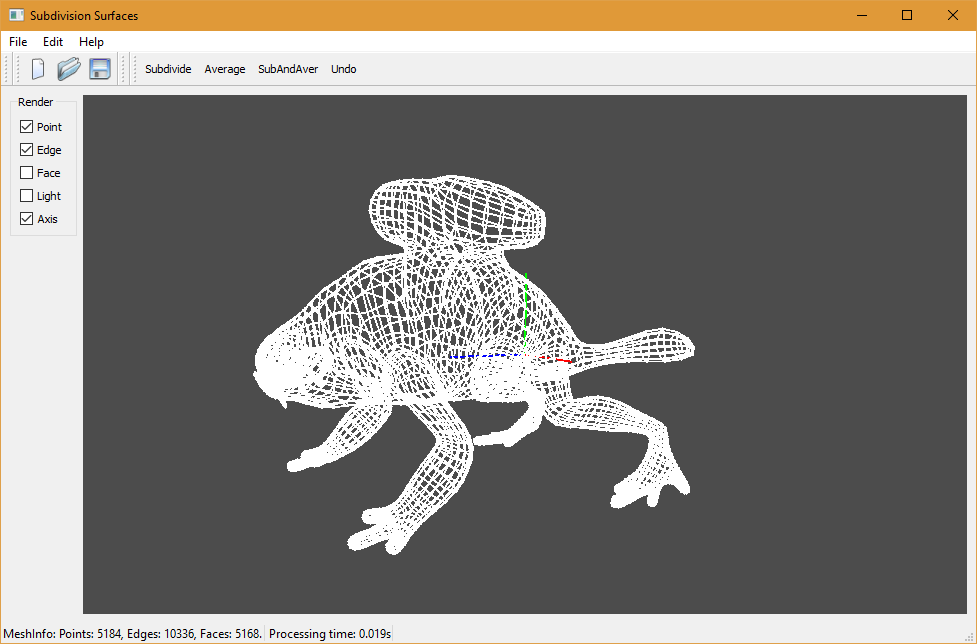
Mesh Subdivision Tool

A simple mesh display and subdivision tool using Qt and OpenGL.

[bin (Win32)] [source (C++)]

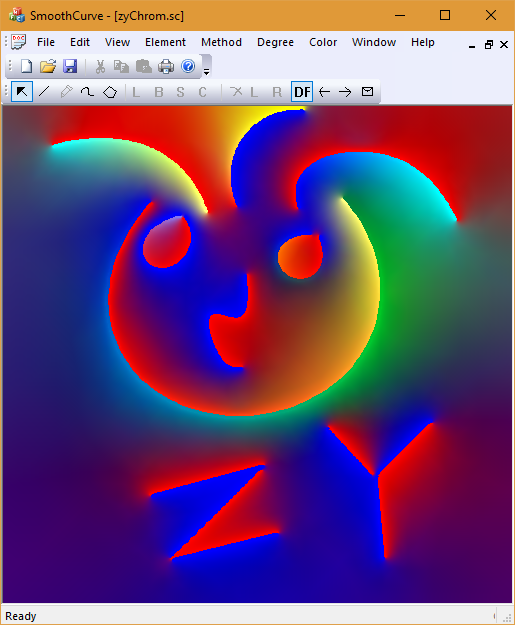
Spline Curves Sketch Board

A simple spline curves drawing board implemented in Microsoft Foundation Class (MFC). Lagrange, Bezier, B-Spline, Catmull-Rom are supported.

A harmonic function is computed with given color along two sides of the curves as constraints.

[Pic]

Study on Segmentation

A paper reading project for mesh segmentation.

A robot for the "24 Game"

Our team "The Mass" won the 3rd place of RoboGame 2012 of USTC in the competition of the "24 Game". Our robot needs to read the 4 numbers on the white board, run to the given location and pick up the pen, then run to the white board and write down how to manipulate the 4 numbers into 24. I did the number reading (OCR) part on a STM32 microcontroller integrated circuit.

Teammates: Jingbei Liu, Qijie Tang, Yuan Cao, Xu Xie

[USTC News]